Which Unit Should Be Studied to Review Symbols From Set Theory? Unit 1 Unit 3 Unit 5 Unit 7

Branch of mathematics that studies sets

Set theory is the co-operative of mathematical logic that studies sets, which tin exist informally described equally collections of objects. Although objects of any kind tin exist collected into a ready, set theory, every bit a branch of mathematics, is by and large concerned with those that are relevant to mathematics equally a whole.

The modern study of set theory was initiated by the German mathematicians Richard Dedekind and Georg Cantor in the 1870s. In particular, Georg Cantor is commonly considered the founder of set up theory. The non-formalized systems investigated during this early stage go under the name of naive ready theory. Afterward the discovery of paradoxes within naive gear up theory (such equally Russell's paradox, Cantor's paradox and Burali-Forti paradox) diverse evident systems were proposed in the early twentieth century, of which Zermelo–Fraenkel gear up theory (with or without the precept of choice) is still the best-known and most studied.

Ready theory is commonly employed as a foundational organisation for the whole of mathematics, particularly in the grade of Zermelo–Fraenkel gear up theory with the precept of choice.^[1] Also its foundational role, set theory as well provides the framework to develop a mathematical theory of infinity, and has various applications in calculator scientific discipline (such as in the theory of relational algebra), philosophy and formal semantics. Its foundational appeal, together with its paradoxes, its implications for the concept of infinity and its multiple applications, take fabricated set theory an area of major interest for logicians and philosophers of mathematics. Contemporary enquiry into gear up theory covers a vast assortment of topics, ranging from the structure of the real number line to the study of the consistency of large cardinals.

History [edit]

Mathematical topics typically emerge and evolve through interactions amongst many researchers. Set up theory, yet, was founded past a unmarried paper in 1874 past Georg Cantor: "On a Property of the Collection of All Real Algebraic Numbers".^[2] ^[3]

Since the 5th century BC, starting time with Greek mathematician Zeno of Elea in the Westward and early on Indian mathematicians in the East, mathematicians had struggled with the concept of infinity. Peculiarly notable is the work of Bernard Bolzano in the first half of the 19th century.^[4] Modernistic understanding of infinity began in 1870–1874, and was motivated by Cantor's work in real analysis.^[5] An 1872 meeting betwixt Cantor and Richard Dedekind influenced Cantor'south thinking, and culminated in Cantor's 1874 paper.

Cantor's work initially polarized the mathematicians of his twenty-four hour period. While Karl Weierstrass and Dedekind supported Cantor, Leopold Kronecker, at present seen equally a founder of mathematical constructivism, did not. Cantorian set theory eventually became widespread, due to the utility of Cantorian concepts, such as one-to-ane correspondence among sets, his proof that in that location are more real numbers than integers, and the "infinity of infinities" ("Cantor'south paradise") resulting from the power fix performance. This utility of set theory led to the commodity "Mengenlehre", contributed in 1898 past Arthur Schoenflies to Klein's encyclopedia.

The adjacent wave of excitement in gear up theory came effectually 1900, when it was discovered that some interpretations of Cantorian set theory gave rise to several contradictions, called antinomies or paradoxes. Bertrand Russell and Ernst Zermelo independently constitute the simplest and best known paradox, now called Russell's paradox: consider "the prepare of all sets that are not members of themselves", which leads to a contradiction since information technology must be a member of itself and not a member of itself. In 1899, Cantor had himself posed the question "What is the central number of the set of all sets?", and obtained a related paradox. Russell used his paradox as a theme in his 1903 review of continental mathematics in his The Principles of Mathematics. Rather than the term set, Russell used the term class, which has subsequently been used more technically.

In 1906, the term set appeared in the volume Theory of Sets of Points ^[6] by hubby and wife William Henry Young and Grace Chisholm Young, published by Cambridge University Press.

The momentum of prepare theory was such that debate on the paradoxes did not lead to its abandonment. The work of Zermelo in 1908 and the piece of work of Abraham Fraenkel and Thoralf Skolem in 1922 resulted in the set up of axioms ZFC, which became the almost commonly used set of axioms for set theory. The piece of work of analysts, such every bit that of Henri Lebesgue, demonstrated the great mathematical utility of set theory, which has since go woven into the fabric of modern mathematics. Set theory is commonly used as a foundational organization, although in some areas—such every bit algebraic geometry and algebraic topology—category theory is thought to be a preferred foundation.

Basic concepts and note [edit]

Set theory begins with a fundamental binary relation betwixt an object $o$ and a set $A$ . If $o$ is a member (or element) of $A$ , the notation $o \in A$ is used. A set is described past listing elements separated past commas, or by a characterizing property of its elements, within braces { }.^[vii] Since sets are objects, the membership relation tin can relate sets also.

A derived binary relation between ii sets is the subset relation, also called set inclusion. If all the members of fix $A$ are also members of set $B$ , then $A$ is a subset of $B$ , denoted $A \subseteq B$ . For example, ${1, 2}$ is a subset of ${i, 2, 3}$ , and and so is ${2}$ but ${1, 4}$ is non. As unsaid past this definition, a set is a subset of itself. For cases where this possibility is unsuitable or would make sense to be rejected, the term proper subset is defined. $A$ is called a proper subset of $B$ if and merely if $A$ is a subset of $B$ , just $A$ is not equal to $B$ . As well, 1, 2, and 3 are members (elements) of the gear up ${1, ii, three}$ , but are non subsets of it; and in turn, the subsets, such as ${1}$ , are not members of the fix ${1, 2, iii}$ .

Only as arithmetic features binary operations on numbers, set theory features binary operations on sets.^[8] The following is a fractional list of them:

Union of the sets $A$ and $B$ , denoted $A \cup B$ , is the fix of all objects that are a fellow member of $A$ , or $B$ , or both.^[9] For example, the matrimony of ${1, 2, 3}$ and ${2, 3, iv}$ is the gear up ${1, 2, three, 4}$ .
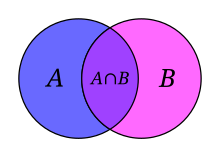
Intersection of the sets $A$ and $B$ , denoted $A \cap B$ , is the fix of all objects that are members of both $A$ and $B$ . For case, the intersection of ${1, 2, 3}$ and ${two, iii, 4}$ is the set ${2, 3}$ .
Set up difference of $U$ and $A$ , denoted $U \ A$ , is the set of all members of $U$ that are not members of $A$ . The set up difference ${ane, 2, 3} \ {ii, iii, iv}$ is ${ane}$ , while conversely, the set difference ${2, three, 4} \ {one, 2, 3}$ is ${4}$ . When $A$ is a subset of $U$ , the set divergence $U \ A$ is also called the complement of $A$ in $U$ . In this case, if the choice of $U$ is clear from the context, the notation $A c$ is sometimes used instead of $U \ A$ , particularly if $U$ is a universal set every bit in the study of Venn diagrams.
Symmetric difference of sets $A$ and $B$ , denoted $A △ B$ or $A ⊖ B$ , is the set of all objects that are a member of exactly i of $A$ and $B$ (elements which are in one of the sets, merely not in both). For example, for the sets ${1, ii, iii}$ and ${2, 3, 4}$ , the symmetric deviation set is ${1, 4}$ . It is the set difference of the union and the intersection, $(A ∪ B) \ (A ∩ B)$ or $(A \ B) ∪ (B \ A)$ .
Cartesian product of $A$ and $B$ , denoted $A \times B$ , is the set whose members are all possible ordered pairs $(a, b)$ , where $a$ is a member of $A$ and $b$ is a member of $B$ . For example, the Cartesian product of {1, 2} and {red, white} is {(ane, red), (one, white), (ii, cherry-red), (2, white)}.
Power set of a set $A$ , denoted ${\mathcal {P}}(A)$ , is the set whose members are all of the possible subsets of $A$ . For example, the power set of ${one, 2}$ is ${ {}, {1}, {two}, {1, two} }$ .

Some basic sets of central importance are the set of natural numbers, the set up of real numbers and the empty set—the unique ready containing no elements. The empty set up is likewise occasionally called the null set,^[x] though this proper name is cryptic and tin can lead to several interpretations.

Some ontology [edit]

An initial segment of the von Neumann hierarchy

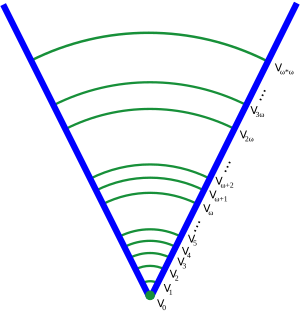
A set is pure if all of its members are sets, all members of its members are sets, so on. For example, the set ${{}}$ containing simply the empty set is a nonempty pure set. In modern set theory, information technology is common to restrict attention to the von Neumann universe of pure sets, and many systems of axiomatic prepare theory are designed to axiomatize the pure sets merely. There are many technical advantages to this restriction, and little generality is lost, because essentially all mathematical concepts can be modeled past pure sets. Sets in the von Neumann universe are organized into a cumulative hierarchy, based on how deeply their members, members of members, etc. are nested. Each ready in this hierarchy is assigned (by transfinite recursion) an ordinal number $\alpha$ , known as its rank. The rank of a pure set $X$ is defined to exist the least ordinal that is strictly greater than the rank of whatsoever of its elements. For case, the empty set is assigned rank 0, while the set ${{}}$ containing only the empty ready is assigned rank 1. For each ordinal $\alpha$ , the fix $V_{\alpha }$ is defined to consist of all pure sets with rank less than $\blastoff$ . The entire von Neumann universe is denoted $Five$ .

Formalized set theory [edit]

Elementary set theory tin can be studied informally and intuitively, and so can be taught in principal schools using Venn diagrams. The intuitive arroyo tacitly assumes that a set may be formed from the class of all objects satisfying any item defining condition. This assumption gives rise to paradoxes, the simplest and best known of which are Russell's paradox and the Burali-Forti paradox. Axiomatic gear up theory was originally devised to rid set theory of such paradoxes.^{[note ane]}

The nigh widely studied systems of axiomatic set theory imply that all sets form a cumulative hierarchy. Such systems come in 2 flavors, those whose ontology consists of:

Sets alone. This includes the most mutual axiomatic set theory, Zermelo–Fraenkel set theory with the axiom of choice (ZFC). Fragments of ZFC include:
- Zermelo set theory, which replaces the axiom schema of replacement with that of separation;
- Full general set theory, a small fragment of Zermelo set theory sufficient for the Peano axioms and finite sets;
- Kripke–Platek set theory, which omits the axioms of infinity, powerset, and choice, and weakens the axiom schemata of separation and replacement.
Sets and proper classes. These include Von Neumann–Bernays–Gödel gear up theory, which has the aforementioned forcefulness every bit ZFC for theorems about sets lonely, and Morse–Kelley fix theory and Tarski–Grothendieck set theory, both of which are stronger than ZFC.

The above systems can be modified to allow urelements, objects that can be members of sets only that are not themselves sets and do not accept any members.

The New Foundations systems of NFU (allowing urelements) and NF (lacking them) are not based on a cumulative hierarchy. NF and NFU include a "gear up of everything", relative to which every ready has a complement. In these systems urelements matter, because NF, but non NFU, produces sets for which the axiom of selection does not hold. Despite NF'due south ontology non reflecting the traditional cumulative hierarchy and violating well-foundedness, Thomas Forster has argued that it does reflect an iterative formulation of fix.^[11]

Systems of constructive set theory, such every bit CST, CZF, and IZF, embed their set axioms in intuitionistic instead of classical logic. Withal other systems accept classical logic but feature a nonstandard membership relation. These include rough set theory and fuzzy set theory, in which the value of an diminutive formula embodying the membership relation is not simply True or Simulated. The Boolean-valued models of ZFC are a related subject.

An enrichment of ZFC called internal set theory was proposed by Edward Nelson in 1977.^{[ citation needed ]}

Applications [edit]

Many mathematical concepts can be defined precisely using only set theoretic concepts. For example, mathematical structures as diverse as graphs, manifolds, rings, vector spaces, and relational algebras can all be defined as sets satisfying various (axiomatic) backdrop. Equivalence and order relations are ubiquitous in mathematics, and the theory of mathematical relations can be described in gear up theory.^{[ citation needed ]}

Set theory is as well a promising foundational system for much of mathematics. Since the publication of the outset volume of Principia Mathematica, it has been claimed that most (or even all) mathematical theorems tin be derived using an aptly designed set of axioms for ready theory, augmented with many definitions, using first or 2d-guild logic. For example, backdrop of the natural and existent numbers can be derived within prepare theory, as each number system can be identified with a set of equivalence classes under a suitable equivalence relation whose field is some infinite set.^{[ citation needed ]}

Prepare theory every bit a foundation for mathematical assay, topology, abstract algebra, and detached mathematics is likewise uncontroversial; mathematicians take (in principle) that theorems in these areas can exist derived from the relevant definitions and the axioms of fix theory. However, it remains that few full derivations of complex mathematical theorems from set theory have been formally verified, since such formal derivations are often much longer than the natural language proofs mathematicians commonly nowadays. One verification projection, Metamath, includes human-written, computer-verified derivations of more than 12,000 theorems starting from ZFC fix theory, first-order logic and propositional logic.^{[ citation needed ]}

Areas of study [edit]

Set theory is a major area of enquiry in mathematics, with many interrelated subfields.

Combinatorial set up theory [edit]

Combinatorial set theory concerns extensions of finite combinatorics to space sets. This includes the study of fundamental arithmetic and the report of extensions of Ramsey'south theorem such as the Erdős–Rado theorem.

Descriptive set theory [edit]

Descriptive ready theory is the study of subsets of the real line and, more by and large, subsets of Polish spaces. It begins with the written report of pointclasses in the Borel bureaucracy and extends to the study of more than circuitous hierarchies such as the projective bureaucracy and the Wadge hierarchy. Many properties of Borel sets can be established in ZFC, but proving these properties concord for more complicated sets requires additional axioms related to determinacy and large cardinals.

The field of effective descriptive set theory is between fix theory and recursion theory. It includes the study of lightface pointclasses, and is closely related to hyperarithmetical theory. In many cases, results of classical descriptive prepare theory have constructive versions; in some cases, new results are obtained past proving the effective version commencement and and then extending ("relativizing") information technology to make it more broadly applicable.

A recent area of research concerns Borel equivalence relations and more complicated definable equivalence relations. This has important applications to the written report of invariants in many fields of mathematics.

Fuzzy set theory [edit]

In set theory as Cantor defined and Zermelo and Fraenkel axiomatized, an object is either a member of a set or not. In fuzzy set theory this status was relaxed by Lotfi A. Zadeh so an object has a degree of membership in a set, a number between 0 and 1. For case, the degree of membership of a person in the set of "tall people" is more than flexible than a unproblematic yeah or no answer and can be a real number such as 0.75.

Inner model theory [edit]

An inner model of Zermelo–Fraenkel set theory (ZF) is a transitive course that includes all the ordinals and satisfies all the axioms of ZF. The canonical example is the constructible universe Fifty developed by Gödel. Ane reason that the study of inner models is of involvement is that it can be used to show consistency results. For example, information technology can be shown that regardless of whether a model V of ZF satisfies the continuum hypothesis or the axiom of pick, the inner model L constructed inside the original model will satisfy both the generalized continuum hypothesis and the axiom of choice. Thus the assumption that ZF is consistent (has at least i model) implies that ZF together with these two principles is consistent.

The written report of inner models is common in the study of determinacy and large cardinals, especially when considering axioms such as the axiom of determinacy that contradict the axiom of choice. Even if a fixed model of set theory satisfies the axiom of choice, it is possible for an inner model to fail to satisfy the axiom of choice. For case, the existence of sufficiently large cardinals implies that there is an inner model satisfying the axiom of determinacy (and thus not satisfying the axiom of choice).^[12]

Large cardinals [edit]

A large cardinal is a key number with an actress property. Many such backdrop are studied, including inaccessible cardinals, measurable cardinals, and many more. These properties typically imply the cardinal number must be very large, with the existence of a cardinal with the specified property unprovable in Zermelo–Fraenkel set theory.

Determinacy [edit]

Determinacy refers to the fact that, under appropriate assumptions, sure 2-player games of perfect information are adamant from the kickoff in the sense that one player must have a winning strategy. The existence of these strategies has important consequences in descriptive set theory, every bit the assumption that a broader class of games is determined often implies that a broader class of sets will have a topological belongings. The axiom of determinacy (AD) is an important object of report; although incompatible with the axiom of pick, Advertising implies that all subsets of the existent line are well behaved (in particular, measurable and with the perfect gear up property). AD tin can be used to prove that the Wadge degrees take an elegant structure.

Forcing [edit]

Paul Cohen invented the method of forcing while searching for a model of ZFC in which the continuum hypothesis fails, or a model of ZF in which the axiom of choice fails. Forcing adjoins to some given model of set theory additional sets in society to create a larger model with properties determined (i.e. "forced") past the structure and the original model. For example, Cohen'due south structure adjoins additional subsets of the natural numbers without changing any of the cardinal numbers of the original model. Forcing is also 1 of two methods for proving relative consistency by finitistic methods, the other method being Boolean-valued models.

Cardinal invariants [edit]

A primal invariant is a property of the existent line measured by a key number. For instance, a well-studied invariant is the smallest cardinality of a collection of meagre sets of reals whose union is the unabridged real line. These are invariants in the sense that any 2 isomorphic models of gear up theory must requite the same cardinal for each invariant. Many cardinal invariants accept been studied, and the relationships between them are oftentimes circuitous and related to axioms of set theory.

Gear up-theoretic topology [edit]

Ready-theoretic topology studies questions of general topology that are set up-theoretic in nature or that crave advanced methods of set theory for their solution. Many of these theorems are independent of ZFC, requiring stronger axioms for their proof. A famous trouble is the normal Moore space question, a question in general topology that was the bailiwick of intense inquiry. The answer to the normal Moore space question was somewhen proved to be independent of ZFC.

Objections to set theory [edit]

From gear up theory'southward inception, some mathematicians have objected to it as a foundation for mathematics. The most common objection to set theory, i Kronecker voiced in gear up theory's earliest years, starts from the constructivist view that mathematics is loosely related to ciphering. If this view is granted, then the handling of infinite sets, both in naive and in evident set up theory, introduces into mathematics methods and objects that are non computable even in principle. The feasibility of constructivism as a substitute foundation for mathematics was greatly increased by Errett Bishop'south influential volume Foundations of Constructive Assay.^[xiii]

A different objection put along by Henri Poincaré is that defining sets using the axiom schemas of specification and replacement, likewise as the axiom of ability set, introduces impredicativity, a type of circularity, into the definitions of mathematical objects. The scope of predicatively founded mathematics, while less than that of the unremarkably accepted Zermelo–Fraenkel theory, is much greater than that of effective mathematics, to the point that Solomon Feferman has said that "all of scientifically applicable analysis tin be developed [using predicative methods]".^[fourteen]

Ludwig Wittgenstein condemned ready theory philosophically for its connotations of mathematical platonism.^[fifteen] He wrote that "set theory is wrong", since information technology builds on the "nonsense" of fictitious symbolism, has "pernicious idioms", and that it is nonsensical to talk about "all numbers".^[xvi] Wittgenstein identified mathematics with algorithmic human deduction;^[17] the need for a secure foundation for mathematics seemed, to him, nonsensical.^[18] Moreover, since homo effort is necessarily finite, Wittgenstein's philosophy required an ontological commitment to radical constructivism and finitism. Meta-mathematical statements — which, for Wittgenstein, included any statement quantifying over space domains, and thus almost all modern set theory — are not mathematics.^[19] Few modern philosophers have adopted Wittgenstein's views afterwards a spectacular blunder in Remarks on the Foundations of Mathematics: Wittgenstein attempted to refute Gödel's incompleteness theorems later on having only read the abstract. As reviewers Kreisel, Bernays, Dummett, and Goodstein all pointed out, many of his critiques did not utilize to the paper in full. Only recently have philosophers such every bit Crispin Wright begun to rehabilitate Wittgenstein's arguments.^[20]

Category theorists have proposed topos theory as an alternative to traditional axiomatic set theory. Topos theory can translate diverse alternatives to that theory, such every bit constructivism, finite ready theory, and computable set theory.^[21] ^[22] Topoi as well give a natural setting for forcing and discussions of the independence of choice from ZF, equally well as providing the framework for pointless topology and Rock spaces.^[23]

An active area of research is the univalent foundations and related to it homotopy type theory. Within homotopy blazon theory, a set may be regarded every bit a homotopy 0-type, with universal properties of sets arising from the inductive and recursive properties of higher inductive types. Principles such as the axiom of choice and the law of the excluded center tin can be formulated in a mode corresponding to the classical formulation in prepare theory or perhaps in a spectrum of singled-out ways unique to type theory. Some of these principles may be proven to exist a consequence of other principles. The multifariousness of formulations of these axiomatic principles allows for a detailed analysis of the formulations required in order to derive diverse mathematical results.^[24] ^[25]

Set theory in mathematical teaching [edit]

Every bit set theory gained popularity as a foundation for modern mathematics, there has been support for the thought of introducing the basics of naive set theory early in mathematics didactics.

In the US in the 1960s, the New Math experiment aimed to teach basic set theory, among other abstract concepts, to principal school students, but was met with much criticism. The math syllabus in European schools followed this tendency, and currently includes the subject at unlike levels in all grades. Venn diagrams are widely employed to explicate basic fix-theoretic relationships to primary school students (even though John Venn originally devised them equally function of a procedure to assess the validity of inferences in term logic).

Set theory is used to introduce students to logical operators (Non, AND, OR), and semantic or rule clarification (technically intensional definition^[26]) of sets (due east.thousand. "months starting with the alphabetic character A"), which may be useful when learning computer programming, since boolean logic is used in various programming languages. Likewise, sets and other collection-like objects, such as multisets and lists, are common datatypes in computer science and programming.

In addition to that, sets are usually referred to in mathematical pedagogy when talking well-nigh different types of numbers ( $N$ , $Z$ , $R$ , ...), and when defining a mathematical part as a relation from one set up (the domain) to another set (the range).

See too [edit]

Glossary of ready theory
Class (set theory)
Listing of set theory topics
Relational model – borrows from prepare theory
Venn diagram

Notes [edit]

^ In his 1925 paper ""An Axiomatization of Fix Theory", John von Neumann observed that "set up theory in its commencement, "naive" version, due to Cantor, led to contradictions. These are the well-known antinomies of the ready of all sets that practice not incorporate themselves (Russell), of the gear up of all transfinite ordinal numbers (Burali-Forti), and the set up of all finitely definable real numbers (Richard)." He goes on to observe that two "tendencies" were attempting to "rehabilitate" set theory. Of the beginning effort, exemplified past Bertrand Russell, Julius König, Hermann Weyl and Fifty. E. J. Brouwer, von Neumann called the "overall effect of their activeness . . . devastating". With regards to the axiomatic method employed past second group equanimous of Zermelo, Fraenkel and Schoenflies, von Neumann worried that "We meet simply that the known modes of inference leading to the antinomies neglect, merely who knows where at that place are not others?" and he set to the chore, "in the spirit of the second group", to "produce, by means of a finite number of purely formal operations . . . all the sets that we want to run across formed" but not allow for the antinomies. (All quotes from von Neumann 1925 reprinted in van Heijenoort, Jean (1967, third press 1976), From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931, Harvard Academy Printing, Cambridge MA, ISBN 0-674-32449-8 (pbk). A synopsis of the history, written past van Heijenoort, can be found in the comments that precede von Neumann's 1925 paper.

References [edit]

^ Kunen 1980, p. xi: "Set up theory is the foundation of mathematics. All mathematical concepts are defined in terms of the archaic notions of set and membership. In axiomatic set theory we formulate a few simple axioms well-nigh these primitive notions in an attempt to capture the basic "obviously true" prepare-theoretic principles. From such axioms, all known mathematics may be derived."
^ Cantor, Georg (1874), "Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen", Journal für die reine und angewandte Mathematik (in German language), 1874 (77): 258–262, doi:x.1515/crll.1874.77.258, S2CID 199545885
^ Johnson, Philip (1972), A History of Set Theory , Prindle, Weber & Schmidt, ISBN0-87150-154-6
^ Bolzano, Bernard (1975), Berg, January (ed.), Einleitung zur Größenlehre und erste Begriffe der allgemeinen Größenlehre, Bernard-Bolzano-Gesamtausgabe, edited by Eduard Winter et al., vol. II, A, 7, Stuttgart, Bad Cannstatt: Friedrich Frommann Verlag, p. 152, ISBN3-7728-0466-seven
^ Dauben, Joseph (1979), Georg Cantor: His Mathematics and Philosophy of the Space, Harvard University Printing, pp. 30–54, ISBN0-674-34871-0 .
^ Young, William; Young, Grace Chisholm (1906), Theory of Sets of Points, Cambridge Academy Printing
^ "Introduction to Sets". world wide web.mathsisfun.com . Retrieved 2020-08-xx .
^ Kolmogorov, A.Due north.; Fomin, S.5. (1970), Introductory Real Analysis (Rev. English ed.), New York: Dover Publications, pp. 2–three, ISBN0486612260, OCLC 1527264
^ "gear up theory | Basics, Examples, & Formulas". Encyclopedia Britannica . Retrieved 2020-08-20 .
^ Bagaria, Joan (2020), "Ready Theory", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Spring 2020 ed.), Metaphysics Enquiry Lab, Stanford University, retrieved 2020-08-xx
^ Forster, T. E. (2008). "The iterative conception of set up" (PDF). The Review of Symbolic Logic. 1: 97–110.
^ Jech, Thomas (2003), Set Theory, Springer Monographs in Mathematics (Third Millennium ed.), Berlin, New York: Springer-Verlag, p. 642, ISBN978-3-540-44085-7, Zbl 1007.03002
^ Bishop, Errett (1967), Foundations of Constructive Assay, New York: Academic Press, ISBN4-87187-714-0
^ Feferman, Solomon (1998), In the Light of Logic, New York: Oxford University Printing, pp. 280–283, 293–294, ISBN0-195-08030-0
^ Rodych, Victor (January 31, 2018). "Wittgenstein's Philosophy of Mathematics". In Zalta, Edward Due north. (ed.). Stanford Encyclopedia of Philosophy (Jump 2018 ed.).
^ Wittgenstein, Ludwig (1975), Philosophical Remarks, §129, §174, Oxford: Basil Blackwell, ISBN0-631-19130-5
^ Rodych 2018, §2.i: "When we prove a theorem or determine a proffer, we operate in a purely formal, syntactical way. In doing mathematics, we practice not discover pre-existing truths that were 'already there without one knowing' (PG 481)—we invent mathematics, bit-by-niggling-flake." Note, however, that Wittgenstein does not place such deduction with philosophical logic; c.f. Rodych §i, paras. 7-12.
^ Rodych 2018, §iii.4: "Given that mathematics is a 'motley of techniques of proof' (RFM III, §46), it does not crave a foundation (RFM VII, §xvi) and it cannot be given a self-axiomatic foundation (PR §160; WVC 34 & 62; RFM IV, §iii). Since set theory was invented to provide mathematics with a foundation, it is, minimally, unnecessary."
^ Rodych 2018, §2.2: "An expression quantifying over an infinite domain is never a meaningful proposition, not even when nosotros have proved, for instance, that a particular number $n$ has a particular property."
^ Rodych 2018, §iii.6.
^ Ferro, Alfredo; Omodeo, Eugenio G.; Schwartz, Jacob T. (September 1980), "Decision Procedures for Elementary Sublanguages of Fix Theory. I. Multi-Level Syllogistic and Some Extensions", Communications on Pure and Practical Mathematics, 33 (5): 599–608, doi:10.1002/cpa.3160330503
^ Cantone, Domenico; Ferro, Alfredo; Omodeo, Eugenio Thou. (1989), Computable Fix Theory , International Series of Monographs on Computer Science, Oxford Science Publications, Oxford, United kingdom of great britain and northern ireland: Clarendon Press, pp. xii, 347, ISBN0-198-53807-3
^ Mac Lane, Saunders; Moerdijk, leke (1992), Sheaves in Geometry and Logic: A Beginning Introduction to Topos Theory, Springer-Verlag, ISBN978-0-387-97710-2
^ homotopy type theory in nLab
^ Homotopy Type Theory: Univalent Foundations of Mathematics. The Univalent Foundations Program. Institute for Advanced Study.
^ Frank Ruda (six October 2011). Hegel's Rabble: An Investigation into Hegel's Philosophy of Right. Bloomsbury Publishing. p. 151. ISBN978-1-4411-7413-0.

External links [edit]

Daniel Cunningham, Set Theory commodity in the Cyberspace Encyclopedia of Philosophy.
Jose Ferreiros, The Early Development of Set Theory article in the [Stanford Encyclopedia of Philosophy].
Foreman, Matthew, Akihiro Kanamori, eds. Handbook of Gear up Theory. 3 vols., 2010. Each chapter surveys some aspect of contemporary enquiry in set up theory. Does not cover established elementary gear up theory, on which see Devlin (1993).
"Axiomatic set theory", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
"Set theory", Encyclopedia of Mathematics, Ems Printing, 2001 [1994]
Schoenflies, Arthur (1898). Mengenlehre in Klein's encyclopedia.
Online books, and library resources in your library and in other libraries nigh set up theory
Rudin, Walter B. (Apr six, 1990). "Set Theory: An Offspring of Analysis". Marden Lecture in Mathematics. Academy of Wisconsin-Milwaukee. Archived from the original on 2021-x-31 – via YouTube.

smithsobsed.blogspot.com

Source: https://en.wikipedia.org/wiki/Set_theory